Consider a rigid body rotating with a constant angular velocity w about an axis through the point O and perpendicular to the plane of the figure. All the particles of the body perform uniform circular motion about the axis of rotation with the same angular velocity ω
Suppose that the body consists of N particles of masses m1, m2, ..., mn, situated at perpendicular distances r1, r2, ..., rn, respectively from the axis of rotation.
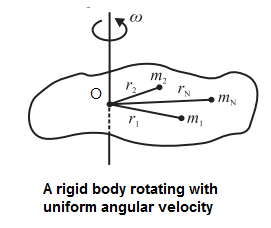
The particle of mass m, revolves along a circle of radius r,, with a linear velocity of magnitude
v1= r1ω The magnitude of the linear momentum of the particle is
p1 = m1v1 = m1r1ω
The angular momentum of the particle about the axis of rotation is by definition,
\(\vec{L_1}=\vec{r_1}\vec{p_1}\)
where θ is the smaller of the two angles between r1 and p1
In this case, θ = 90° ∴ sinθ = 1
∴ L1 = r1 p1 = r1m1r1ω = m1r12ω
Similarly, L2 = m2r22ω, L3 = m3r32ω etc.
The angular momentum of the body about the given axis is
L= L1 + L2 +L3 ……. + LN
= m1r12ω + m2r22ω + m3r32ω …….. mNrN2ω
= ω (m1r12 + m2r22 + m3r32 …….. mNrN2)
\(=(\sum \limits_{i=1}^{N}m_ir_i^2)ω\)
= moment of inertia of the body about the given axis.
In vector form, L⃗ =Iω⃗
Thus, angular momentum = moment of inertia x angular velocity.
Note: Angular momentum is a vector quantity. It has the same direction as ω⃗