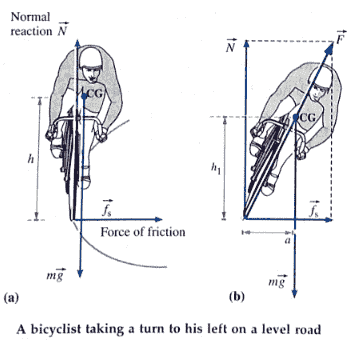
(i) When a bicyclist takes a turn along an unbanked road, the force of friction \(\vec{Fs}\) provides the centripetal force; the normal reaction of the road \(\vec{N}\) is vertically up. If the bicyclist does not lean inward, there will be an unbalanced outward torque about the centre of gravity, fs·h, due to the friction force that will topple the bicyclist outward. The bicyclist must lean inward to counteract this torque (and not to generate a centripetal force) such that the opposite inward torque of the couple formed by and the weight g, mg·a = fs·h1.
(ii) Since the force of friction provides the centripetal force,
,\(f_s=\frac{mv^2}{r}\)
If the cyclist leans from the vertical by an angle q, the angle between N⃗ and F⃗ as shown in fig (b).
\(\frac{f_s}{N}\ = \frac{mv^2/r}{mg}=\frac{v^2}{gr}\)
Hence, the cyclist must lean by an angle
θ =\(\tan^{-1}\frac{v^2}{gr}\)

(iii) When a car takes a turn along a level road, apart from the risk of skidding off outward, it also has a tendency to roll outward due to an outward torque about the centre of gravity due to the friction force. But a car is an extended object with four wheels, So, when the inner wheels just pet lifted above the ground, it can be counterbalanced by a restoring torque of the couple formed by the normal reaction (on the outer wheels) and the weight.