Question

In the given figure, if LK = 6$\sqrt{3}$ , find MK, ML, KN, MN and the perimeter of $◻$MNKL.

Answer 1

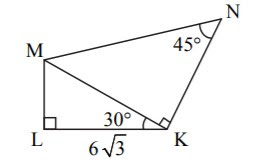
Solution::

In $\mathrm{△}LKM$ , 

$tan{30}^{\circ }=\frac{ML}{LK}$

$\Rightarrow ML=6\sqrt{3}\times {\displaystyle \frac{1}{\sqrt{3}}}=6$

$\cos {30}^{\circ }=\frac{LK}{MK}$

$\Rightarrow MK={\displaystyle \frac{LK}{\cos {30}^{\circ }}}={\displaystyle \frac{6\sqrt{3}}{{\displaystyle \frac{\sqrt{3}}{2}}}}=12$

 

NK=MK (Side opposite to equal angles )

$\therefore NK=12$

In$\mathrm{△}MKN$

$\sin {45}^{\circ }={\displaystyle \frac{NK}{MN}}$

${\displaystyle \frac{1}{\sqrt{2}}}={\displaystyle \frac{12}{MN}}$

$MN=12\sqrt{2}$

Perimeter of ◻MNKL =MN+NK+Lk+ML 

$perimeter=12\sqrt{2}+12+6\sqrt{3}+6$

$=18+6(2\sqrt{2}+\sqrt{3})$ unit {if cm then cm}

Video solution ::

Comments

create video solution for this sum !!!