A particle of mass m with an initial velocity collides perfectly elastically with a mass 3 m at rest. It moves with a velocity

Question

A particle of mass m with an initial velocity \(u\hat{\text{i}}\) collides perfectly elastically with a mass 3 m at rest. It moves with a velocity \(v\hat{\text j}\)after collision, then, vv is given by  

a)  \(v=\sqrt{2\over3}u\) 

b)  \(v= {u\over\sqrt3}\) 

c)  \(v={u\over\sqrt6 }\) 

d)  \(v={u\over\sqrt2}\)

Answer 1

The correct answer is option d) \(v={u\over \sqrt 2 }\) 

Explaination ::

 

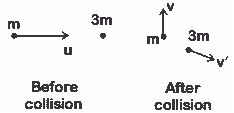
\(mu\hat{i}+0=mv\hat{j}+3m\hat{v'}\)

\(\hat{v'}={u\over3}\hat{i}-{v\over3}\hat{j}\)  

\({1\over2}mu^2={1\over2}mv^2+{1\over2}(3m)\Big(\big({u\over3}\big)^2+\big({v\over3}\big)^2\Big)\)   --------{ K.E.}

\(mu^2=m(v^2+({u^2\over 3}+{v^2\over3})\)

\(u^2=(v^2+{u^2\over 3}+{v^2\over3})\)

\(3u^2-3v^2=u^2+v^2\)

\(2u^2=4v^2\)

\(u^2=2v^2\)

\(v={u\over\sqrt2}\)