Definition : The radius of gyration of a body rotating about an axis is defined as the distance between the axis of rotation and the point at which the entire mass of the body can be supposed to be concentrated so as to give the same moment of inertia as that of the body about the given axis.
The moment of inertia (MI) of a body about a given rotation axis depends upon
1. the mass of the body and
2. the distribution of mass about the axis of rotation. These two factors can be separated by expressing the MI as the product of the mass (M) and the square of a particular distance (k) from the axis of rotation. This distance is called the radius of gyration and is defined as given above. Thus,
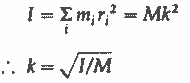
Physical significance :The radius of gyration is less if I is less, i.e., if the mass is distributed close to the axis; and it is more if I is more, i.e., if the mass is distributed away from the axis. Thus, it gives the idea about the distribution of mass about the axis of rotation.
The centre of mass (CM) coordinates locates a point where if the entire mass M of a system of particles or that of a rigid body can be thought to be concentrated such that the acceleration of this point mass obeys Newton’s second law of motion, viz.,
\(\overrightarrow{F_{net}}\) = M \(\overrightarrow{a_{CM}}\), where \(\overrightarrow{F_{net}}\) is the sum of all the external forces acting on the body or on the individual particles of the system of particles.
Similarly, radius of gyration locates a point from the axis of rotation where the entire mass M can be thought to be concentrated such that the angular acceleration of that point mass about the axis of rotation obeys the relation, \(\vec{\tau _{net}}\) = M\(\vec{\alpha}\) , where \(\vec{\tau _{net}}\) is the sum of all the external torques acting on the body or on the individual particles of the system of particles.