Given, d(X, Y) = 17, d(Y, Z) = 8
Case I: Points X, Y, Z are such that, X – Y – Z.
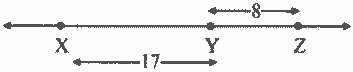
∴ d(X, Z) = d(X, Y) + d(Y, Z) = 17 + 8
∴ d(X, Z) = 25
Case II:Points X, Y, Z are such that, X – Z – Y.

∴ d(X,Y) = d(X,Z) + d(Z,Y)
∴ 17 = d(X, Z) + 8
∴ d(X, Z) = 17 – 8
∴ d(X, Z) = 9
Case III:Points X, Y, Z are such that, Z – X – Y.

From the diagram,
d(X, Y) > d (Y, Z)
Which is not possible
∴ Point X is not between Z and Y.
∴ d(X, Z) = 25 or d(X, Z) = 9.