An ideal simple pendulum is defined as a heavy point mass suspended from a rigid support by a weightless, inextensible and twistless string, and set oscillating under gravity through a small angle in a vertical plane.
In practice, a small but heavy sphere, called the bob, is used. The distance from the point of suspension to the centre of gravity of the bob is called the length of the pendulum.
Consider a simple pendulum of length L1 – suspended from a rigid support O. When displaced from its initial position of rest through a small angle θ in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in below figure. At B, the forces on the bob are its weight \(m \vec{g}\) and the tension \(\overrightarrow{F_{1}}\) in the string. Resolve \(m \vec{g}\) into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string.
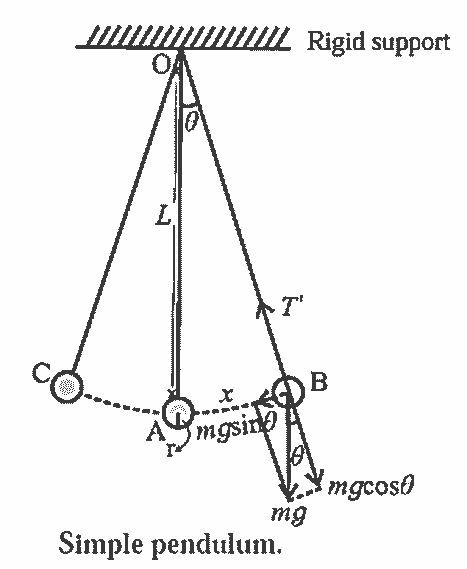
mg cos θ balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position.
Restoring force, F = – mg sin θ
If θ is small and expressed in radian,
sin θ \(\approx\) θ = \(\frac{\text { arc }}{\text { radius }}\) = \(\frac{\mathrm{AB}}{\mathrm{OB}}\) = \(\frac{x}{L}\)
∴ F = – mgθ = -mg\(\frac{x}{L}\) …. (1)
Since m, g and L are constant,
F ∝ (-x) …. (2)
Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM.
Acceleration, a = \(\frac{F}{m}\) = –\(\frac{g}{L}\)x … (3)
Therefore, acceleration per unit displacement
= |\(\frac{a}{x}\)| = \(\frac{g}{L}\) ….. (4)
Period of SHM,
T = \(\frac{2π}{\sqrt{\text{acceleration per unit displacement}}}=\frac{2π}{\sqrt{g/L}}\)
∴ T = \(2π\sqrt{L/g}\)
This gives the expression for the period of a simple pendulum.