Let ∆ABC be the given equilateral triangle.
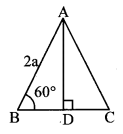
∴ ∠B = 60° [Angle of an equilateral triangle]
Let AD ⊥BC, B – D – C.
In ∆ABD, ∠B = 60°, ∠ADB = 90°
∴ ∠BAD = 30° [Remaining angle of a triangle]
∴ ∆ABD is a 30° – 60° – 90° triangle.
∴ AD = \(\frac{\sqrt{3}}{2}\) AB [Side opposite to 60°]
= \(\frac{\sqrt{3}}{2}\) × 2a
= a\(\sqrt { 3 }\) units
The height of the equilateral triangle is a\(\sqrt { 3 }\) units.