Question

One of the diameter of the circle circumscribing the rectangle ABCD is 4y = x + 7. If A and B are the points (-3, 4) and (5, 4) respectively, then find the area of rectangle

Answer 1

Let O be the centre of circle M be mid point of AB.

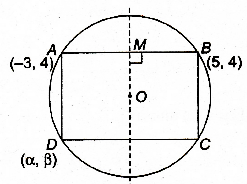
Then , OM \(\perp\) AB \(\Rightarrow\) M (1,4)

Since, slope of AB = 0

Equation of straight line MO is x = 1 and equation of diameter is \(4y = x + 7\).

\(\Rightarrow\) Centre is (1, 2).

Also, O is mid point of BD

\(\Rightarrow(\frac{\alpha+5}{2},\frac{\beta+4}{2})=(1,2)\)

\(\Rightarrow\alpha =-3,\beta =0\)

\(\therefore AD=\sqrt{(-3+3)^2+(4-0)^2}=4\)

and \(AB=\sqrt{64+0}=8\)

Thus, area of rectangle is \(8\times4=32\;sq\;unit\)