What is Linear Regression?
Linear Regression is a machine learning algorithm it is used for predicting Dependent variable based on independent variables. Equation:- y=w*X+b
How Linear Regression work?
Linear regression is based on concept of line. Equation of line is y=m*x+c, where m is slope and c is constant in machine learning we call them weight(w) and bias(b) respectively, y and x are dependent and independent variable respectively. So now based on x we can predict y. Example:- if x=2 then y=m*2+c. (Independent variable is always present in question statement).
How to find values of m, c?
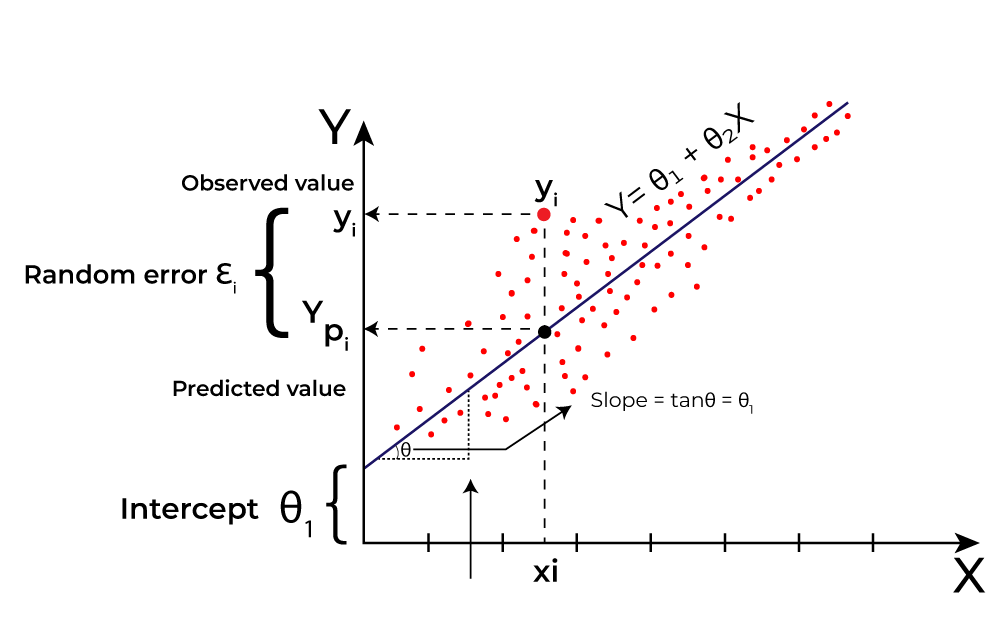
To answer this question we will fit a line on a dataset.
Step 1:-
Initialize W and b at random. For this purpose you can use numpy.random.randn() or similar other functions like zeros(),ones(), rand() present in Numpy Library. or you can use functions from Tensorflow.
weights = np.zeros((1,1))
bias = 0Step 2:-
perform forward prop using W and b.
Forward Prop:-
y=w*X+b
# code for forward prop:-
y_pred=W*X+bStep 3:-
Calculate loss function:-
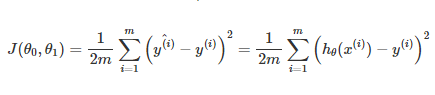
cost=1/(2*m)*np.sum(np.square(y_pred-Y)) # Y is actual value of Independent variable were as y_pred value is predicted value of Independent value variable using forward prop.Step 4:-
Find dw and db
dw and db are slope of cost function with respect to w and b
reduce dw and db from w and b at a certain called as learning rate (lr). this step is known as Back-prop
#Code for dw and db
dw=(1/m)*np.sum(X*y_pred-Y)
db=(1/m)*np.sum(y_pred-Y)
W = W - lr * dw
b = b - lr * db
Step 5:-
Repeat step 2 and step 4 till cost function is not almost zero and there you have perfect values of W and b.
Predict:-
y_pred = np.dot(X, W) + bCode For LinearRegression Model:-
class LinearRegression:
def __init__(self, lr=0.0001, n_iters=100):
self.lr = lr
self.n_iters = n_iters
self.weights = None
self.bias = None
def fit(self, X, y):
n_samples, n_features = X.shape
self.weights = np.zeros((1,1))
self.bias = 0
for _ in range(self.n_iters):
y_pred = np.dot(X, self.weights) + self.bias
print(1/(2*25000)*np.sum(np.square(y_pred-Y)))
dw = (1/n_samples) * np.dot(X.T, (y_pred-y))
db = (1/n_samples) * np.sum(y_pred-y)
print(dw.shape)
print(db.shape)
self.weights = self.weights - self.lr * dw
self.bias = self.bias - self.lr * db
def predict(self, X):
y_pred = np.dot(X, self.weights) + self.bias
return y_predAfter adding Sigmoid activation you can modify linear Regression to logistic Regression.
