Draw a block diagram of the Error Back Propagation Algorithm

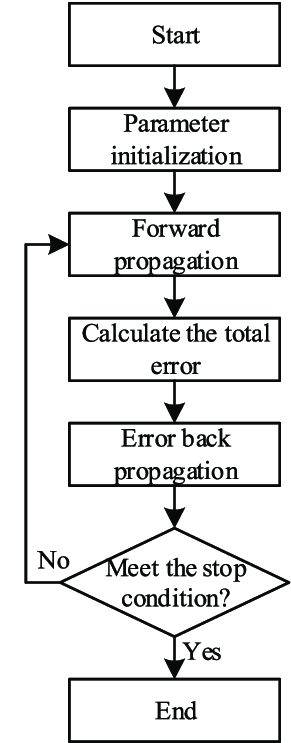
The Error Back Propagation Algorithm, commonly referred to as Backpropagation, is a fundamental algorithm used for training artificial neural networks. It is a supervised learning algorithm that aims to minimize the error between the predicted outputs and the actual outputs by adjusting the weights of the network.

1. Neural Network Structure:
   • Input Layer: Receives input features.
   • Hidden Layers: Intermediate layers where computations are performed.
   • Output Layer: Produces the final output.
2. Weights and Biases: Parameters that the algorithm adjusts to minimize the error.
3. Activation Function: A non-linear function (like Sigmoid, ReLU, Tanh) applied to the neuron’s output to introduce non-linearity into the model.
4. Loss Function: Measures the difference between the predicted output and the actual output (e.g., Mean Squared Error, Cross-Entropy Loss).

Steps in Backpropagation

1. Initialization: Randomly initialize weights and biases.
2. Forward Propagation:
   • Compute the output of each neuron from the input layer to the output layer.
   • For each layer, apply the activation function to the weighted sum of inputs.
3. Compute Loss: Calculate the error using the loss function.
4. Backward Propagation:
   • Compute the gradient of the loss function with respect to each weight by applying the chain rule of calculus.
   • This involves:
   • Output Layer: Calculate the gradient of the loss with respect to the output.
   • Hidden Layers: Backpropagate the gradient to previous layers, updating the weights and biases.
5. Update Weights:
   • Adjust weights and biases using gradient descent or an optimization algorithm (like Adam, RMSprop).
   • Update rule:
     [
     w = w – \eta \frac{\partial L}{\partial w}
     ]
     where ( \eta ) is the learning rate, ( w ) is the weight, and ( \frac{\partial L}{\partial w} ) is the gradient of the loss with respect to the weight.
6. Iterate: Repeat the forward and backward pass for a number of epochs or until convergence.

Practical Considerations

• Learning Rate: A critical hyperparameter that needs to be set properly. Too high can lead to divergence, too low can slow convergence.
• Overfitting: Use techniques like regularization (L1, L2), dropout, or early stopping to prevent overfitting.
• Gradient Vanishing/Exploding: Deep networks may suffer from these issues. Techniques like Batch Normalization, appropriate activation functions (ReLU), and gradient clipping help mitigate them.